1 映射与函数
邻域定义:以点x0为中心的任何开区间为点x0的邻域,记为U(x0)。
δ邻域定义:设δ为一正数,则称开区间(x0−δ,x0+δ)为点x0的δ邻域,记作U(x0,δ)。x0称为邻域的中心,δ为邻域的半径。
去心δ邻域就是去除x0的δ邻域,记为U˚(x0,δ),左δ邻域就是左侧的去心δ邻域,记为U+(x0,δ),右δ邻域就是右侧的去心δ邻域,记为U−(x0,δ)。
邻域定义:设点P0(x0,y0)为xOy平面上的一点,δ为某一个正数,与点P0(x0,y0)的距离小于δ的点P(x,y)的全体,称为点P0的δ邻域,记为U(P0,δ)。
同理可以得到去心δ邻域的定义。
δ邻域的几何意义:以P0(x0,y0)为中心,以δ>0为半径的圆内部所有的点。
函数的邻域就是一个区间,所以比如函数在某点的某邻域内有定义,就是说明函数在这个点的附近有定义,这个附近的距离没有必要说明。
函数的概念
- 函数即y=f(x),x∈D,x为自变量,y为因变量,D为定义域。
- 一个x对应一个y,一个y可能对应多个x。
反函数
y=f(x),定义域为D,值域为R,若对于每一个y∈R,必然存在x∈D使y=f(x)成立,则可以定义一个新函数x=ψ(y),这个函数就是y=f(x)的反函数,一般记作x=f−1(y),其定义域为R,值域为D,对于反函数,原来的函数称为直接函数。
- 严格单调函数必然有反函数,即函数导数恒正或恒负必然有反函数。
- x=f−1(y)与y=f(x)在同一坐标系中完全重合。
- y=f−1(x)与y=f(x)关于y=x对称。
- f[f−1(x)](f[ψ(x)])或f−1[f(x)]=x(ψ[f(x)])变为x,称为湮灭。
可以验算一下性质四。
已知y=ex和y=lnx是一对反函数,y=lnex=f−1(f(x))=x。
反�函数的求法:
- 求值域。
- 求解。(用y表示x)
- 互换xy。
例题:若函数y=f(x)的反函数为y=f−1(x),则求y=f(2x−1)+1的反函数的解析式。
解:整理y=f(2x−1)+1,得到f(2x−1)=y−1,所以求反函数就是交换xy。
这里将2x−1当作x,y−1当作y,所以得到反函数2x−1=f−1(y−1)。
所以得到x=2f−1(y−1)+1。
所以交换表示方法其反函数就是y=2f−1(x−1)+1。
2 数列的极限
数列极限定义
设{xn}为一数列,若存在常数a,对于不论任意小的ξ>0,总存在正整数N,使n>N时,∣xn−a∣<ξ恒成立,则常数a为数列{xn}的极限,或{xn}收敛于a,记为:x→∞limxn=a或xn→a(n→∞)。
x→∞limxn=a⇔∀ξ>0,∃N∈N+,当n>N时,恒有∣xn−a∣<ξ。
注意到:定义中的正整数N是与任意给定的整数ξ有关的,它随着ξ的给定而选定。
极限证明
令xn为通项,a为极限值,ξ为任意正数。
-
写出∣xn−a∣<ξ。
-
反解出项数n<g(ξ)。
-
取N=[g(ξ)]+1,所以令n>N就可以证明。
例题:用定义证明x→∞lim[1+n(−1)n]=1
证明:计算距离:1+n(−1)n−1=n(−1)n<ξ。
解得到:n1<ξ,反解为n>ξ1。
取整(存在取一个即可):N=[ξ1]+1。
∴∀ξ>0,当n>N时,使得1+n(−1)n−1=n(−1)n<ξ。
∴证明完毕。
例题:用定义证明n→∞limqn=0(q为常数且∣q∣<1)。
证明:∣qn−0∣<ξ。
∣qn∣<ξ,取对数进行反解nln∣q∣<lnξ,又因为∣q∣<1,所以ln∣q∣<0,所以得到n>ln∣q∣lnξ。
(若ξ>1则 n 大于一个负数,即是存在这个正整数n的,这样条件必然成立)
∴∀ξ∈(0,1) 取N=[ln∣q∣lnξ]+1。
∴当n>N时,必然n>ln∣q∣lnξ,有∣qn−0∣<ξ。
故n→∞limqn=0。
这里为什么不用证明ξ≥1这种情况?是因为其判断条件∣qn−0∣<ξ的ξ小于更小的数,即大于1这个数也必然成立。
数列绝对��值
定理:若x→∞liman=A,则x→∞lim∣an∣=∣A∣。
证明:∵n→∞liman=A⇔∀ξ>0,∃N>0,当n>N,恒有∣an−A∣<ξ。
又由重要不等式∣∣a∣−∣b∣∣⩽∣a−b∣,所以∣∣an∣−∣A∣∣⩽ξ。
所以恒成立,证明完毕。
从这个题推出:n→∞liman=0⇔n→∞lim∣an∣=0。所以如果我们以后需要证明某一数列极限为0,可以证明数列绝对值极限0,而数列绝对值绝对时大于等于0的,所以由夹逼准则,其中小的一头已经固定为0了,所以只用找另一个偏大的数列夹逼所证明数列就可以了。
唯一性
定义:若数列{xn}收敛于a,则a是唯一的。
证明:设n→∞liman=A且n→∞liman=B且A=B。
不如设A>B。任意取ξ=2A−B>0。
∵n→∞liman=A
∴∃N1>0,当n>N1时,∣an−A∣<2A−B。
得到2A+B<an<23A−B并设为式子一。
又∵n→∞liman=B
∴∃N2>0,当n>N2时,∣an−B∣<2A−B。
得到23A−B<an<2A+B�并设为式子二。
取N=max{N1,N2},当n>N时,式子一二同时成立,而A=B,则这两个式子不可能同时成立,矛盾��。
同理A<B时也矛盾,所以A=B矛盾。
证明数列是发散的
令xn为通项,a为极限值,ξ为任意正数。
- 取ξ的范围在一个区间内
- 证明数列的所有值都在这个区间外面
有界性
定义:若数列{xn}极限存在,则数列有界。
即n→∞liman=A,则存在M>0,使得∣an∣⩽M。
证明:由极限定义,取ξ=1。
∵n→∞liman=A
∴∃N>0,当n>N时,∣an−A∣<1。
∵重要不等式∣∣an∣−∣A∣∣⩽∣an−A∣
∴n>N时,∣∣an∣−∣A∣∣<1⇒∣an∣<1+∣A∣
取M=max{∣a1∣,∣a2∣,⋯,∣aN∣,1+∣A∣}
∀n,有∣an∣⩽M
所以数列极限存在则数列有界。但是数列有界不一定极限存在,如1+(−1)n。
推论:收敛 ⇒ 有界,有界 ⇏ 收敛,无界 ⇒发散,发散 ⇏ 无界
保号性
较重要。也称为脱帽法。
定义:若数列{xn}存在极限n→∞liman=a=0,则存在正整数N,当n>N时an都与a同号。
简单来说,就是极限大于0,后面一部分数列大于0,极限小于0,后面一部分数列小于0。
推论,戴帽法:若数列{an}从某项开始an⩾b,且n→∞liman=a,则a⩾b。这里一定要带等号。
证明:设A>0,取ξ=2A>0。
∵n→∞liman=A
∴∃N>0,当n>N时,∣an−A∣<2A⇒an>2A>0
同理得证极限值小于0的情况。
子数列
定义:从数列an:a1,a2,⋯,an,⋯中选取无穷多项并按原来顺序组成的新数列就称为原数列的子列,记为{ank}:an1,an2,⋯,ank,⋯。
若nk分别取奇数和偶数,则得到奇数项数列与偶数项数列。也就是说子列是按照顺序下来取的数列,顺序不改变,但间隔可以改变。
定理:若数列{an}收敛,则其任何子列{ank}也收敛,且极限值相同。
所以对于其变式我们用到更多:
- 若一个数列{an}能找到一个发散的子列,那该数列发散。
- 若一个数列{an}能找到两个极限值不同的收敛子列,那么这个数列发散。
- 若一个数列{an},则其奇数子列与偶数子列都收敛于同一个值。
例如对于数列{(−1)n},能找到其奇数子列收敛于-1,偶数子列收敛于1,所以收敛值不同,原数列发散。
3 函数的极�限
函数极限定义
极限定义
定义:设函数f(x)在点x0的某一个去心邻域有定义,若存在常数A,对于任意给定的ξ>0,总存在正数δ,使得当0<∣x−x0∣<δ式,对应的函数值f(x)都满足不等式∣f(x)−A∣<ξ,则A就是函数f(x)当x→x0时的极限,记作x→x0limf(x)=A或f(x)→A(x→x0)。
x→x0limf(x)=A⇔∀ξ>0,∃δ>0,当0<∣x−x0∣<δ时,有∣f(x)−A∣<ξ。
而对于趋向无穷时:x→∞limf(x)=A⇔∀ξ>0,∃X>0,当∣x∣>X时,有∣f(x)−A∣<ξ。
注意:这里的趋向分为六种:x→x0、x→x0+、x→x0−、x→∞、x→∞+、x→∞−。
单侧极限
当x→x0−存在的极限称为左极限,当x→x0+存在的极限称为右极限。
函数极限存在条件
函数存在的充要条件是:
- x→x0limf(x)⇔x→x0−limf(x)=x→x0+limf(x)=A。
- 函数脱帽法:x→x0limf(x)⇔f(x)=A+α(x),x→x0limα(x)=0,后面的α(x)就是函数与极限值的误差。
极限情况总结
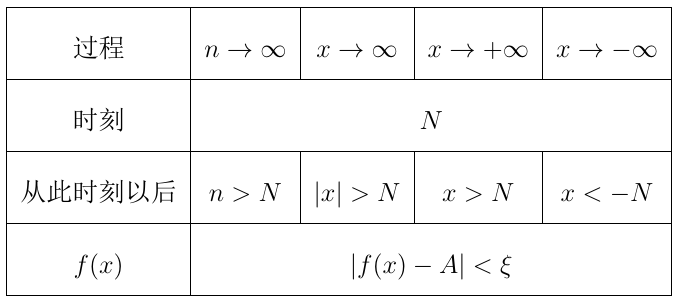

与数列极限性质类似,且任何x的趋向三个性质都是成立的。
唯一性
定义:若极限存在,则极限唯一。
局部有界性
定义:若极限存在且为A,则存在正常数M和δ,使得当0<∣x−x0∣<δ时,有∣f(x)∣⩽M。
-
极限存在是函数局部有界性的充分不必要条件。
-
f(x)在[a,b]上连续,则f(x)在[a,b]上有界。
-
有限个有界函数与有界函数的和、差、积仍是有界函数。
-
若f′(x)在有限区间(a,b)内有界,则f(x)在该区间内有界。
对于结论二,可以利用极限存在必然连续的概念,对f(x)在区间两端求极限从而证明有界。这里两端的极限不要求是一样的,因为两端不一样的极限表明该趋向点的极限值不存在,但是仍然有界。
证明结论四:
利用中值定理:f(b)−f(a)=f′(ξ)(b−a)。
令x∈(a,b),x0∈(a,b)。其中这两个值不知道大小,只知道范围。
代入中值定理:f(x)−f(x0)=f′(ξ)(x−x0)
∣f(x)∣=∣f(x0)+f′(ξ)(x−x0)∣⩽∣f(x0)∣+∣f′(ξ)∣∣x−x0∣ (重要绝对值不等式)⩽∣f(x0)∣+K⋅(b−a)⩽M
